今天做笔试题，遇到一道题目，题目如下：

题目描述
对于不同的字符串，我们希望能有办法判断相似程度，我们定义了一套操作方法来把两个不相同的
字符串变得相同，具体的操作方法如下：
1 修改一个字符，如把“a”替换为“b”。
2 增加一个字符，如把“abdd”变为“aebdd”。
3 删除一个字符，如把“travelling”变为“traveling”。
比如，对于“abcdefg”和“abcdef”两个字符串来说，我们认为可以通过增加和减少一个“g”的方式
来达到目的。上面的两种方案，都只需要一次操作。把这个操作所需要的次数定义为两个字符串
的距离，而相似度等于“距离＋1”的倒数。也就是说，“abcdefg”和“abcdef”的距离为1，
相似度为1/2=0.5.
给定任意两个字符串，你是否能写出一个算法来计算出它们的相似度呢？

状态转移方程

粗略想了一下，应该是用动态规划的方法来做吧，但是具体这个状态转移方程怎么写呢？还是先来分析一下，假设我们有两个字符串:

str\_a=(a1, a2, ..., ai), 
str\_b=(b1, b2, ..., bj), 
L(a, b)表示把字符串a和b变成相同字符串所需要的操作次数

如果(a1 == b1)，则L(str_a, str_b) = L(str_a[2, len(str_a)], str_b[2, len(str_b)])
如果(a1 != b1)，则L(str_a, str_b) = min{L1, L2, L3}，其中
L1 = L(str_a[1, len(str_a)], str_b[2, len(str_b)]) // 删去str_b的一个字符
L2 = L(str_a[2, len(str_a)], str_b[1, len(str_b)]) // 删去str_a的一个字符
L3 = L(str_a[2, len(str_a)], str_b[2, len(str_b)]) // 修改str_a的一个字符(或str_b的一个字符)
因此我们可以通过上述的状态转移方程来构造一个二位的表来查找最长公共子序列。

例子1

下面以一个例子来说明：
str_a = “abcdef”, str_b = “bdf”
第一步构造一个二维矩阵，其中x表示空，显然我们可以先把矩阵的第一行和第一列先赋好值，如下图所示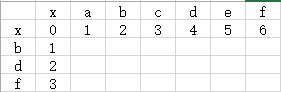

下面来构造矩阵的第二行，首先看(b, a)，由于(b != a)所以找 min{(x, x), (x, a), (b, x)} = 0，因此(b, a) = 0 + 1 = 1。这里+1是因为(b != a)，所我们需要一步使它们相等(b变a，a变b都行)。
再看(b, b)，由于(b == b)，所以(b, b) = (x, a) = 1。
接着看(b, c)，由于(b != c)，所以找 (b, c) = min{(x, b), (x, c), (b, b)} + 1 = 2。
……
这样我们就构造好了第二行。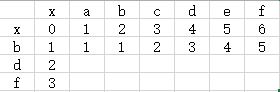

之后是完整的矩阵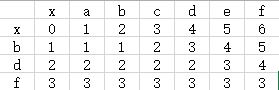

因此，要使str_a = str_b， 我们需要变动3次，即矩阵最右下角的数字。

代码

下面是用c++实现的动态规划的代码

#include <iostream>
#include <string>
#include <vector>
using namespace std;
inline int min(int a, int b, int c)
{
	if (a < b)
	{
		if (a < c) return a;
		else return c;
	}
	else
	{
		if (b < c) return b;
		else return c;
	}
}
int main(void)
{
	
	string str1, str2;
	while (cin >> str1 >> str2)
	{
		vector<vector<int>> dp_table(str1.length() + 1, vector<int>(str2.length() + 1, 0));	
		// 第一行
		for (int i = 0; i <= str1.length(); ++i)
		{
			dp_table[i][0] = i;
		}
		// 第一列
		for (int j = 0; j <= str2.length(); ++j)
		{
			dp_table[0][j] = j;
		}
		// dp
		for (int i = 1; i <= str1.length(); ++i)
		{
			for (int j = 1; j <= str2.length(); ++j)
			{
				if (str1[i - 1] == str2[j - 1])
				{
					dp_table[i][j] = dp_table[i - 1][j - 1];
				}
				else
				{
					dp_table[i][j] = min(dp_table[i - 1][j], dp_table[i][j - 1], dp_table[i - 1][j - 1]) + 1;
				}
			}
		}
		cout << "1/" << dp_table[str1.length()][str2.length()] + 1 << endl;
	}
	return 0;
}

最长公共子序列

与上述问题相似的另一类问题叫最长公共子序列(LCS)问题：一个数列 ，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则称为已知序列的最长公共子序列。这里的序列是不要求连续的，解法和上面的问题非常类似。
同样的，先来分析一下状态转移方程。设我们有两个字符串str1 = (a1, a2, …, ai), str2 = (b1, b2, …, bj)， L(a, b)是字符串a,b的最长公共子序列的长度。这次我们从字符串的尾部看：
如果(ai == bj)，L(str1, str2) = L(str1[1, i - 1], str2[1, j - 1]) + 1,
否则的话，L(str1, str2) = max{L1, L2, L3}，其中
L1 = L(str1[1, i], str2[1, j - 1])
L2 = L(str1[1, i - 1], str2[1, j])
L3 = L(str1[1, i - 1], str2[1, j - 1])
也就是说在这三种可能中找到最长的那种可能，正好和上一问题的解法相反。

例子2

下面还是用一个直观的例子来说明问题，还是以上面那两个字符串为例 str1 = “abcdef”, str2=“bdf”。
构造初始的二维矩阵：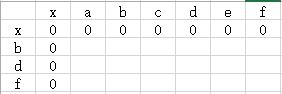

同样的，x表示空字符，这里的第一行和第一列初始化为0，这个也很好理解，任何字符串和一个空的字符串的最长公共子序列长度当然为0。
接下来构造第二行。
由于(b != a)， 因此(b, a) = max{(x, x), (x, a), (b, x)} = 0;
由于(b == b)， 因此(b, b) = (x, a) + 1 = 1;
由于(b != c)， 因此(b, c) = max{(x, b), (x, c), (b, b)} = 1；
以此类推，知道构造完整个矩阵。矩阵最右下角的数值即为最长公共子序列的长度。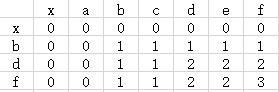

代码

没有代码，根据以上内容，结合第一个问题的代码稍作修改就可以得出第二个问题的代码了。:)