什么是例子滤波

“估计”就是从带有随机误差的观测数据中估计出某些参数或某些状态变量。估计问题一般分为三类：从当前和过去的观测值来估计信号的当前值，称为滤波；从过去的观测值来估计信号的将来值，称为预测或外推；从过去的观测值来估计过去的信号值，称为平滑或内插。滤波理论就是在对系统可观测信号进行测量的基础上，根据一定的滤波准则，对系统的状态或参数进行估计的理论和方法。
粒子滤波（Particle Filtering）是英国学者Gordon，Salmond等于1993年提出的基于Bayesian原理的非参数化序贯蒙特卡洛(Sequential Monte Carlo methods)模拟递推滤波算法，其核心是利用一些随机样本（粒子）来表示系统随机变量的后验概率分布，适合于强非线性、非高斯噪声系统模型的滤波。Kalman滤波是Bayesian估计在线性条件下的实现形式，而粒子滤波是Bayesian估计在非线性条件下的实现形式。

粒子滤波作为跟踪的基本框架

粒子滤波作为跟踪的基本框架，主要可以分为4个主要步骤，即初始化阶段，搜索阶段，决策阶段，重采样阶段。
1. 初始化阶段
程序手动或自动选择一块跟踪区域，计算该区域的特征向量。比如，这个特征可以是颜色，那么可以用颜色直方图来可以表示为一个特征向量。同时我们也初始化N个粒子(Particle)，并为它们初始状态赋值，比如位置可以就是这块被跟踪区域的中心，大小就是被跟踪区域的大小等。最后还要给这些粒子赋权重，由于我们认为初始化的时候，这些粒子的重要性是一样的，所以每个粒子的权重都为1/N。
2. 搜索阶段
看网上有些博客中把这一阶段解释为放狗，我认为很接地气。这一阶段我们放出一些狗去搜寻我们需要跟踪的目标，这里的狗就是粒子。撒例子的方法有很多种，比如
(1)均匀的放(uniform distribution)：在整个搜寻区域内均匀地撒例子；
(2)按高斯分布撒粒子(gaussian distribution)：在靠近目标的区域内多放一些粒子。这些粒子撒出去之后，在以它们各自为中心，目标大小的矩形区域内计算图像的颜色直方图，并与原目标颜色直方图之间比较，计算出两个直方图之间的距离。显然，两个直方图之间的距离越小，那么他们的相似度就越高。这里计算直方图之间的距离方法也很多，比如最常用的巴氏距离(Bhattacharyya distance)。然后对这些相似度做一个归一化操作，使他们的和为1。同时，我们还需要根据每个粒子与目标之间的相似度来重新计算每个粒子的权重。

3. 决策阶段
这个阶段，我们撒出去的粒子要向我们报告他们的状态了。比如1号粒子报告，它所在区域和目标的相似度为0.1，2号粒子报告它所在区域和目标的相似度为0.2，3号粒子报告它所在的区域和目标的相似度为0.3……这里的相似度为上一步中计算得到的。那么我们可以综合这些粒子报告的信息来猜测出目:标的实际位置，即对这些粒子报告的信息做一下加权平均

$$x=\sum_{i=1}^n x_i*w_i$$
$$y=\sum_{i=1}^n y_i*w_i$$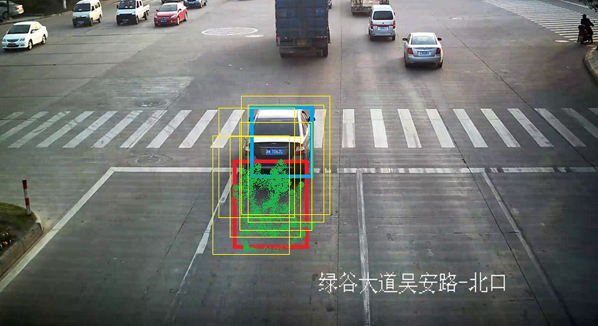

4. 重采样阶段
由于目标的运动是不确定的，我们如果漫无目的地让这些粒子去搜寻，显然效果不会太好，所以我们要重新分布这些粒子。那么怎么分布这些粒子呢？由于那些权重较高的粒子很有可能比较接近目标，所以我们在权重较高的粒子附近多撒一些粒子，而在权重较低的地方收回一些粒子，使粒子的总数保持不变。
这就是Improtance Sampling。
现在我们只要循环(2)->(3)->(4)…就得到了一个目标的跟踪过程。

---

《An Adaptive Color-Based Particle Filter》

上面这篇是我在学习粒子滤波算法的时候看到的一篇写得非常好的论文。值得一提的是这篇论文是在2002年发表的，所以我目前的研究和国外还是相差好远啊。好了，回到正题，下面将结合这篇论文来深入理解一下粒子滤波。

1. Particle Filter
粒子滤波最初是被用来在复杂的环境中来跟踪物体的。被跟踪物体的状态可以用向量\(X_t\)来表示，物体到t时刻的观测状态可以用向量\(Z_t=\lbrace z_1,\ldots,z_t\rbrace\)来表示。粒子滤波常用于后验概率\(p(X_t|Z_t)\)和观测概率\(p(Z_t|X_t)\)是非高斯的情况。

粒子滤波的核心思想是用粒子的权重分布来近似概率分布，其中粒子的权重分布可以用集合\(S=\lbrace (S^\left (n \right ),\pi^\left (n\right ))|n=1\ldots N\rbrace\)来表示。每一个粒子S表示一个对目标状态的猜测，并且猜测的置信度为\(\pi\)，其中\(\sum_{n=1}^N \pi^\left (n\right ) = 1\)。

2. Color Distribution Model
由于颜色分布模型有着鲁棒性，能够应对非刚性，旋转以及部分遮挡等问题而常被用于对目标建模。我们把颜色分布均匀地映射到m个bin中。颜色直方图通过函数\(h(x_i)\)得到，函数\(h(x_i)\)的作用是把位于\(x_i\)位置的像素点的颜色映射到对应的bin中。在作者的实验中，颜色直方图有\(8*8*8\)个bin。如果希望算法不收到光照变化的影响的话，也可是使用HSV模型来替代RGB模型，比如把V分量的bin数量减少为4。(\(8*8*4\)个bin)。

同时为了提升颜色分布模型的可靠度，使物体边缘的背景像素或者被遮挡时的像素减少对模型的影响，作者还设计了一个核函数
$$k(r)=\left \lbrace {1-r^2:r<1} \atop {0:\text{otherwise}} \right . $$
其中\(r\)是像素点距离中心的距离。

颜色分布\(p_y = {\lbrace p_y^\left (u\right ) \rbrace}_{u=1\ldots m} \)在\(y\)点的值可以通过下式计算出：
$$p_y^\left (u \right ) = f\sum_{i=1}^I k\left ( \frac{|y-x_i|}{a}\right ) {\delta [h(x_i)-\mu]}$$
其中\(I\)是该区域内像素点的个数，\(\delta\)是Kronecker delta函数，参数\(a=\sqrt{H_x^2 + H_y^2}\)是该区域的半径。归一化因子
$$f=\frac{1}{\sum_{i=1}^I k\left ( \frac{|y-x_i|}{a} \right )}$$
用来确保\(\sum_{u=1}^m p_y^{\left ( u \right )} = 1\)。

在每一次的跟踪迭代中，我们都需要一个方法来测量观察结果的相似度。一个很经典的测量向量\(p(u)\)和\(q(u)\)之间距离的方法是Bhattacharyya coefficient
$$\rho[p,q]=\int \sqrt{p(u)q(u)}du$$
对于离散的密度，比如两个颜色直方图\(p={\lbrace p^{(u)} \rbrace}_{u=1 \ldots m}\)和\(q={\lbrace q^{(u)} \rbrace}_{u=1 \ldots m}\)的coefficient可以定义为
$$\rho[p,q]=\sum_{u=1}^m \sqrt{p^{(u)}q^{(u)}}$$
\(\rho\)的值越大，则两个直方图之间的相似度越接近。对于两个相同的分布，令\(\rho=1\)来代表完美匹配。对于两个分布，作者定义了Bhattacharyya distance
$$d=\sqrt{1-\rho[p,q]}$$

3. Color-Based Particle Filtering
在跟踪的过程中，使用Bhattacharyya distance来更新先验概率。每一个样本的分布用下式来表示：
$$s=\lbrace x,y,\dot{x},\dot{y},H_x,H_y,\dot{a}\rbrace$$
其中\(x,y\)是区域的中心位置，\(\dot{x},\dot{y}\)是速度，\(H_x,H_y\)是区域的半宽和半高，\(\dot{a}\)是尺度变换率。粒子通过下面这个动态模型来传播：
$$s_t=As_{t-1}+w_{t-1}$$
其中\(A\)是模型的状态空间，\(w_t-1\)是一个多元高斯随机变量。在作者的系统中，使用一个一阶模型来描述一个区域的运动，物体的运动速度为常量\(\dot{x},\dot{y}\)，物体的尺度变化率为\(\dot{a}\)。

作者使用粒子所在位置的颜色直方图和目标的颜色直方图之间的Bhattacharry coefficient来计算粒子的权重。计算公式如下：
$$\pi^{(n)}=\frac1{\sqrt{2\pi}\sigma}e^{-\frac{d^2}{2\sigma ^2}} = \frac1{\sqrt{2\pi}\sigma} e^{-\frac{\left (1-\rho[p_{s^{(n)}},q]\right )}{2\sigma^2}}$$

4. Target Model Update
由于光照条件，可视角度以及相机参数等都会影响color-based particle filter的跟踪效果。为了克服这些问题，作者在跟踪的过程中缓慢更新目标模型。为了防止在物体被遮挡或者噪声太大的时候更新目标模型，作者设置了一个更新条件阈值
$$\pi_{E[S]}>\pi_T$$
其中\(\pi_{E[S]}\)是平均状态\(E[S]\)的观测概率，\(\pi_T\)是一个阈值.
目标模型通过下式得到更新：
$$q_t^{(u)}=(1-\alpha )q_{t-1}^{(u)}+\alpha p_{E[S_t]}^{(u)}$$

完整的算法流程请查看论文，论文中有整个算法过程的描述。

实现效果

我根据上文中的这篇论文以及[1]中作者的代码，用EmguCV实现了一个基于颜色分布的粒子滤波。总的来说跟踪的精确性还行，能应对部分遮挡，跟踪物体状态突然发生变化等情况。当选中的跟踪区域较小时，可以达到实时跟踪，但是当选择区域较大时，计算量急剧增加，效率降低，达不到实时的要求，代码还有改进的空间。下图是效果：

改进方向

粒子滤波目前主要的研究方向为：
1.改进粒子滤波的重采样算法，提高效率；
2.粒子数量的自适应取值算法。

应用领域

目前粒子滤波的主要应用领域有：

1. 视觉跟踪领域
2. 目标定位、导航、跟踪领域
3. 通信与信号处理领域
4. 其他领域

Reference

1. http://blog.csdn.net/jinshengtao/article/details/30970733
2. http://www.cnblogs.com/yangyangcv/archive/2010/05/23/1742263.html
3. Nummiaro K, Koller-Meier E, Van Gool L. An adaptive color-based particle filter[J]. Image and vision computing, 2003, 21(1): 99-110.
4. 王法胜, 鲁明羽, 赵清杰, 等. 粒子滤波算法[J]. 计算机学报, 2014, 37(8): 1679-1693.